기본형 타입 중 정수형과 실수형에 대해 알아보자
2024. 12. 23. 13:00ㆍJAVA
728x90
반응형
안녕하세요. 진득코딩입니다.
이번 시간에는 저번 시간에 이어 기본형 타입에 대해서 살펴보도록 하겠습니다.
그중에서도 숫자들을 다루는 정수형과 실수형에 대해 알아보겠습니다.
정수형 ( byte, short, int, long)
- 정수형에는 모두 4개의 자료형이 있으며, 기본 자료형(default data type)은 int입니다.
- 어떤 진법의 리터럴을 변수에 저장해도 실제로는 2진수로 바뀌어 저장됩니다.
- 2진수가 저장되는 형식은 크게 정수형과 실수형이 있습니다.
| S | n-1 bit |
S : 부호 비트(양수는 0, 음수는 1)
n : 타입의 크기(단위: bit)
- 모든 정수형은 부호 있는 정수이므로 왼쪽의 첫 번째 비트를 부호 비트(sign bit)로 사용하고, 나머지는 값을 표현하는 데 사용합니다.
- 그래서 n비트로 표현할 수 있는 값의 개수인 2^n에서, 절반인 0으로 시작하는 2^n-1개의 값을 양수(0도 포함)의 표현에 사용하고, 나머지 절반인 1로 시작하는 2^n-1개의 값은 음수의 표현에 사용합니다.
| 정수형의 표현형식(n bit) | 종류 | 값의 개수 | |
| 0 | n-1 bit | 0, 양수 | 2^n-1개 |
| 1 | n-1 bit | 음수 | 2^n-1개 |
- 정수형은 타입의 크기만 알면, 최대값과 최솟값을 쉽게 계산할 수 있습니다.
n비트로 표현할 수 있는 정수의 개수 : 2^n개 ( = 2^n-1개 + 2^n-1개)
n비트로 표현할 수 있는 부호있는 정수의 범위 : -2^(n-1) ~ 2^(n-1)-1
- 정수의 범위에서 1을 빼는 이유는 범위에 0이 포함되기 때문입니다.
정수형의 선택 기준
- byte나 short를 사용하게 되면 메모리를 조금 더 절약할 수 있지만, 연산 시에 범위를 넘어서 잘못된 결과를 얻기 쉽기 때문에 byte나 short보다는 int를 사용하는 것이 좋습니다.
- 또한 JVM의 피연산자 스택(operand stack)이 피연산자를 4byte 단위로 저장하기 때문에 크기가 4byte보다 작은 자료형(byte, short)의 값을 계산할 때는 4byte로 변환하여 연산을 수행하게 되기 때문에 오히려 int를 사용하는 것이 더 효율적입니다.
- int타입의 크기는 4byte(=32bit)이므로, 표현할 수 있는 정수의 개수는 2^32 ≃ 4*10^9, 약 40억이며 표현 가능한 정수의 범위는 -2^31 ~ 2^31-1 ≃ +-20억입니다.
2^10 = 1024 ≃ 10^3이므로, 2^32 = 2^10 * 2^10 * 2^10 * 2^2 = 1024 * 1024 * 1024 * 4 ≃ 4 * 10^9
- 정리하자면 정수형 변수를 선언할 때는 int타입으로 하고, int의 범위 (약 20억)를 넘어서 수를 다뤄야 한다면 long을 사용합니다.
- byte나 short은 성능보다 저장공간을 절약하는 것이 더 중요할 때 사용합니다.
- long 타입의 범위를 벗어나는 값을 다룰 때는, 실수형 타입이나 BigInteger 클래스를 사용합니다.
정수형의 오버플로우
- 타입이 표현할 수 있는 값의 범위를 넘어서는 것을 오버플로우(overflow)라고 합니다.
- 에러가 발생하는 것은 아니지만 예상했던 결과를 얻지 못합니다.
- 최대값에 1을 더하면 최솟값이 되고, 최솟값에서 1을 빼면 최댓값이 됩니다.
최대값 + 1 -> 최솟값
최솟값 -1 -> 최댓값
부호 있는 정수의 오버플로우
- 부호 없는 정수는 2진수로 0000이 될 때 오버플로우가 발생하고, 부호 있는 정수는 부호 비트가 0에서 1일 될 때 오버플로우가 발생합니다.
- 부호없는 정수의 경우 표현 범위가 0 ~ 15이므로 이 값이 계속 반복되고, 부호있는 정수의 경우 표현 범위가 -8 ~ -7이므로 이 값이 무한히 반복됩니다.

- 최솟값에서 1을 빼면 최댓값이 되고, 최댓값에 1을 더하면 최솟값이 된다는 것을 확인할 수 있습니다.
- short과 char의 크기는 모두 16bit이므로 표현할 수 있는 값의 개수 역시 2^16개(65536개)로 같습니다.
- short은 이 중에서 절반(2^15개 = 32768개)을 음수를 표현하는 데 사용하고, char는 전체(2^16개 = 65535+1개)를 양수(65535개)와 0(1개)을 표현하는데 사용합니다.
16비트로 표현할 수 있는 정수의 개수 : 2^16개 ( 65536개 )
short타입의 표현범위 : -2^15 ~ 2^15-1 ( -32768 ~ 32767 )
char타입의 표현범위 : 0 ~ 2^16-1 ( 0 ~ 65535 )
실수형 (float, double)
- 실수형은 실수를 저장하기 위한 타입으로 float와 double, 두 가지가 있으며 각 타입의 변수에 저장할 수 있는 값의 범위는 아래 표와 같습니다.
| 타입 | 저장 가능한 값의 범위(양수) | 정밀도 | 크기 | |
| bit | byte | |||
| float | 1.4 * 10^(-45) ~ 3.4 * 10^38 | 7자리 | 32 | 4 |
| double | 4.9 * 10^(-324) ~ 1.8 * 10^308 | 15자리 | 64 | 8 |
- 위 표의 범위는 양의 범위만 적은 것으로, 이 범위에 -부호를 붙이면 음의 범위가 됩니다.
- float타입의 표현 범위는 -3.4*10^38 ~ 3.4 * 10^38이지만, -1.4*10^(-45) ~ 1.4*10^(-45) 범위 (0은 제외)의 값은 표현할 수 없습니다.
- 실수형은 얼마나 0에 가깝게 표현할 수 있는가도 중요합니다.
- 실수형에서는 오버플로우가 발생하면 변수의 값은 무한대(infinity)가 됩니다.
- 그리고 정수형에는 없는 언더플로우(underflow)도 있는데 이는 실수형으로 표현할 수 없는 아주 작은 값, 즉 양의 최솟값보다 작은 값이 되는 경우를 말합니다.
- 이때 변수의 값은 0이 됩니다.
| int : 1 + 31 = 32( 4 byte) | |
| S(1) | 31 bit |
| float : 1 + 8 + 23 = 32(4 byte) | ||
| S(1) | E(8) | M(23) |
- int타입은 부호와 값 두 부분으로 이루어져 있지만, float타입과 같은 실수형은 부호(S), 지수(E), 가수(M), 세 부분으로 이루져 있습니다.
- 즉 2의 제곱을 곱한 형태(+-M * 2^E)로 저장하기 때문에 이렇게 큰 범위의 값을 저장하는 것이 가능합니다.
- 그러나 실수형은 오차가 발생할 수 있다는 단점이 있습니다.
- 그래서 실수형에서는 정밀도(precision)도 중요한 요소입니다.
- float타입은 정밀도가 7자리인데, 이는 7자리의 10지수를 오차 없이 저장할 수 있다는 뜻입니다.
- 7자리 이상의 정밀도가 필요하다면, 변수의 타입을 double로 해야 합니다.
- float타입이 아닌 double타입의 변수를 사용하는 경우는 대부분 보다 높은 정밀도가 필요해서입니다.
- 연산속도의 향상이나 메모리를 절약하려면 float를 선택하고, 더 큰 값의 범위가 필요하거나 더 높은 정밀도를 필요로 한다면 double을 선택해야 합니다.

- %f는 기본적으로 소수점 이하 6자리까지만 출력합니다.
- %24.20f는 전체 24자리 중에서 20자리는 소수점 이하의 수를 출력하라는 뜻입니다.
- float타입의 변수 f에 저장하려던 원래의 값은 9.12345678901234567890이지만 저장공간의 한계로 오차가 발생하여 실제 저장된 값은 9.12345695495605500000입니다.
- 이때 정밀도가 7자리이므로 두 값의 앞의 7자리는 일치하는 것을 확인할 수 있습니다.
실수형의 저장형식
- 실수형은 값을 부동소수점수(floating-point)의 형태로 저장합니다.
- 부동소수점수는 실수를 '+-M*2^E'와 같은 형태로 표현하는 것을 말합니다.
- 부동소수점수는 부호(sign), 지수(Exponent), 가수(Mantissa)로 이루어져 있습니다.
| float : 1 + 8 + 23 = 32(4 byte) | ||
| S(1) | E(8) | M(23) |
| double : 1 + 11 + 52 = 64 (8 byte) | ||
| S(1) | E(11) | M(52) |
- 위와 같은 표현형식은 IEEE754라는 표준을 따른 것인데, IEEE754는 전기 전자 기술자 협회(IEEE, Institute of Electrical and Electronics Engineers)에서 제정한 부동수소점수의 표현 방법이다.
| 기호 | 의미 | 설명 |
| S | 부호(Sign bit) | 0이면양수, 1이면 음수 |
| E | 지수(Exponent) | 부호있는 정수, 지수의 범위는 -127 ~ 128(float), -1023 ~ 1024(double) |
| M | 가수(Mantissa) | 실제 값을 저장하는 부분. 10진수로 7자리(float), 15자리 (double)의 정밀도로 저장 가능 |
- 부호(Sign bit)
- S는 부호비트(sign bit)를 의미하며 1bit입니다.
- 이 값이 0이면 양수를, 1이면 음수를 의미합니다.
- 실수형은 2의 보수법을 사용하지 않기 때문에 양의 실수를 음의 실수로 바꾸려면 그저 부호비트만 0에서 1로 변경하면 됩니다. - 지수(Exponent)
- E는 지수를 저장하는 부분으로 float의 경우, 8bit의 저장공간을 갖습니다.
- 지수는 부호 있는 정수이고 -127 ~ 128의 값이 저장됩니다.
- 이 중에서 -127과 128은 숫자 아님(NaN, Not a Number)이나 양의 무한대(POSITIVE_INFINITY), 음의 무한대(NEGATIVE_INFINITY)와 같이 특별한 값의 표현을 위해 예약되어 있으므로 실제로 사용가능한 지수의 범위는 -126~127입니다.
- 지수의 최댓값이 127이므로 float타입으로 표현할 수 있는 최댓값은 2^127이고, 10진수로 약 10^38입니다.
- 그러나 float의 최솟값은 가수의 마지막 자리가 2^(-23)이므로 지수의 최솟값보다 2^(-23)배나 더 작은 값, 약 10^(-45)입니다. - 가수(Mantissa)
- M은 실제 값인 가수를 저장하는 부분으로 float의 경우, 2진수 23자리를 저장할 수 있습니다.
- 2진수 23자리로는 약 7자리의 10진수를 저장할 수 있는데 이것이 바로 float의 정밀도가 됩니다.
- double은 가수를 저장할 수 있는 공간이 52자리로 float보다 약 2배이므로 double이 float보다 약 2배의 정밀도를 갖습니다.
부동소수점의 오차
- 실수 중에는 무한소수가 존재하므로, 정수와 달리 실수를 저장할 때는 오차가 발생할 수 있습니다.
- 또한 2진수로 변환하면 무한소수가 되는 경우도 있습니다.
- 2진수로 변환된 실수를 저장할 때는 먼저 1.xxx * 2^n의 형태로 변환하는데, 이 과정을 정규화라고 합니다.
- 지수는 기저법으로 저장되기 때문에, 지수인 3에 기저인 127을 더한 130이 2진수로 변환되어 저장됩니다.
- 기저법은 2의 보수법처럼 부호 있는 정수를 저장하는 방법입니다.
- 저장할 때 특정값(기저)을 더했다가 읽어올 때는 다시 뺍니다.
- 최대오차는 약 2^(-23)인데 이 값은 가수의 마지막 비트의 단위와 같습니다.
- 2^(-23)은 10진수로 0.0000001192(약 2^-23)이므로 float의 정밀도가 7자리인 것입니다.
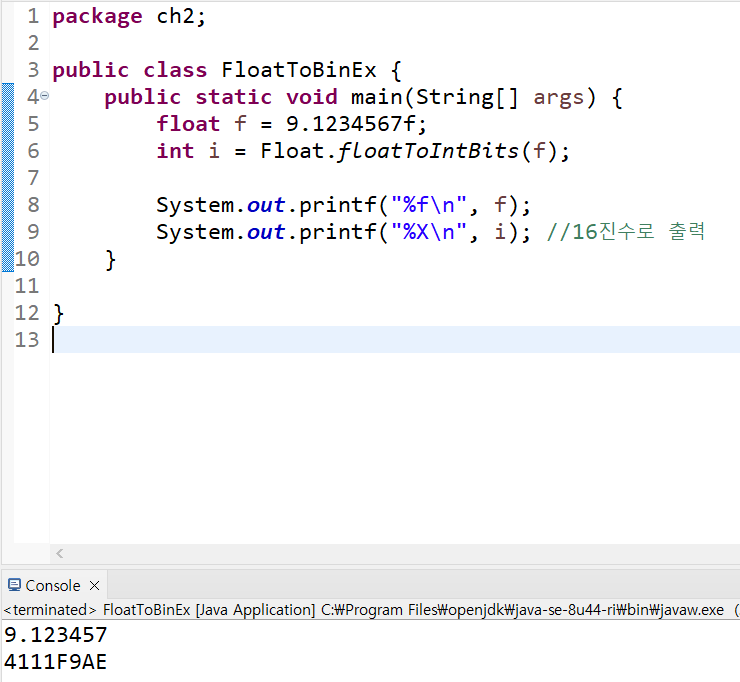
- Float클래스의 floatToIntBits()는 float타입의 값을 int타입의 값으로 해석해서 반환합니다.
- 위 예제에서 두 번째 출력값이 0x4111F9AE인 이유는 잘려나간 첫 번째 자리의 값이 1이라서 반올림되어 0x4111F9AD의 2진수 마지막 자리 두 자리의 값이 01에서 10으로 증가했기 때문입니다.
- 10진수와 달리 2진수는 1이면 반올림하는데, 이는 2진수에서는 1이 절반이기 때문입니다.
이번 시간에는 기본 자료형 중 숫자를 다루는 정수형과 실수형에 대해서 살펴보았습니다.
정수형은 4가지, 실수형에는 2가지 타입이 있기 때문에 상황에 따라 적절한 자료형을 사용해 좋은 프로그램을 만드는 개발자가 됩시다.
이번 포스팅은 여기까지입니다.
끝까지 봐주셔서 감사합니다.😊
728x90
반응형
LIST
'JAVA' 카테고리의 다른 글
| 자바 연산자(operator) 개념과 종류에 대해 알아보자 (0) | 2024.12.26 |
|---|---|
| 형변환으로 다른 타입으로 변환해보자 (0) | 2024.12.24 |
| 기본형 타입 중 논리형과 문자형에 대해 알아보자 (4) | 2024.12.20 |
| 진법을 이용하여 숫자를 여러 방식으로 표현해보자 (0) | 2024.12.19 |
| 자바 console에 입출력을 해보자 (0) | 2024.12.18 |